Intercambiar filas y columnas de una matriz en MATLAB

El hecho de intercambiar filas y columnas de una matriz suele ser un tema muy importante en álgebra lineal. Aquí vamos a explicar con ejemplos cómo lograr esto mediante la indexación de matrices utilizando el operador dos puntos.

Para ejemplificar vamos a utilizar la matriz A, definida por:

$$A=\begin{bmatrix} 1 & 2 & 3 \\ 4 & 5 & 6  \\ 7 & 8 & 9 \end{bmatrix}$$

Creando la matriz en MATLAB:

>> A=[1,2,3;4,5,6;7,8,9]
A =
     1     2     3
     4     5     6
     7     8     9

Intercambiar filas

Suponga que se pide intercambiar las filas 1 y 2, entonces se procedería como sigue:

>> A([1 2],:)=A([2 1],:)
A =
     4     5     6
     1     2     3
     7     8     9

Básicamente le estamos "diciendo" a MATLAB que de la matriz A sustituya todas las columnas de las filas 1 y 2 por las filas 2 y 1, es decir, "invirtiendo" el orden.


Intercambiar columnas

La lógica usada es prácticamente la misma que en el caso anterior, con la única diferencia que el operador dos puntos lo utilizaremos en el índice de las filas. Por ejemplo, de la matriz A original vamos a intercambiar las filas 2 y 3:

>> A(:,[2 3])=A(:,[3 2])
A =
     1     3     2
     4     6     5
     7     9     8


Definiendo funciones propias

Finalmente, si lo anterior le parece un poco confuso, puede utilizar las siguientes funciones: swaprows y swapcols, que intercambian filas y columnas respectivamente:

function X = swaprows(A,m1,m2)

X = A;

X(m1,:) = A(m2,:);

X(m2,:) = A(m1,:);

end

function X = swapcols(A,n1,n2)

X = A;

X(:,n1) = A(:,n2);

X(:,n2) = A(:,n1);

end

La sintaxis para ambas es similar, simplemente necesita pasar como argumento la matriz y las filas y/o columnas a intercambiar de posición. Desde luego las funciones anteriores no están incluidas en MATLAB por defecto, por lo que habrá de colocarlas a su directorio de trabajo o bien añadirlas al PATH de MATLAB.

GUIOOD Toolbox, desarrollando GUIs utilizando el paradigma de la POO

GUIOOD Toolbox (Graphical User Interface with Object-Oriented Design) es un conjunto de clases implementadas en MATLAB cuyo objetivo es desarrollar interfaces gráficas de usuario utilizando una sintaxis similar a la de Java, es decir, con el paradigma de la programación orientada a objetos. 

Básicamente, GUIOOD se está desarrollando para funcionar como un wrapper de las GUIs ordinarias en MATLAB. Se pretende que la programación de GUIs sea más rápida y sencilla. Desde luego que habrá de considerarse el hecho de que "debajo" hay una interfaz gráfica ordinaria, por lo cual la cantidad de controles gráficos disponibles serán los mismos, con algunos añadidos utilizando la librería swing de Java.

¿Qué es lo nuevo?

Desde luego, la forma de programar. Todos los elementos gráficos serán objetos de una determinada clase y tendrán métodos para modificar sus atributos. Por ejemplo para crear una ventana el código correspondiente sería algo como esto:

app = Frame('Ventana 1', [300 200]);

app.SetColor('r');

Ha de mencionarse que el nombre de algunos controles gráficos han sido sustituidos por su equivalente en Java, además que muchos métodos guardan similitud con dicho lenguaje y en otros casos con la librería wxPython. La siguiente es una tabla que muestra la equivalencia de notación entre las GUIs MATLAB ordinarias y el GUIOOD Toolbox:

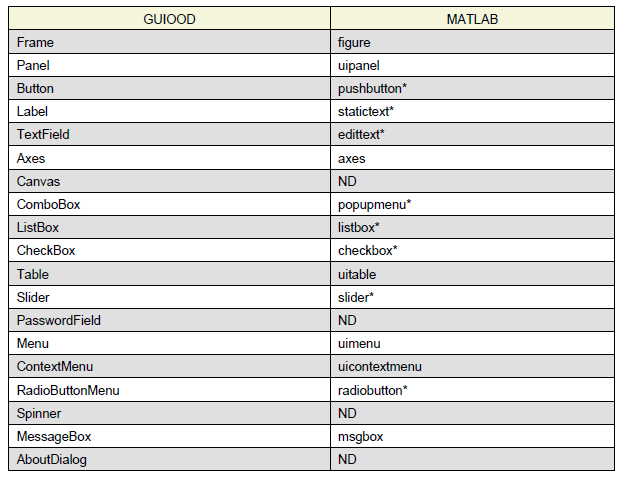
Como puede verse en la tabla, GUIOOD añade algunos controles gráficos no disponibles en MATLAB. El Canvas es un axes "modificado" que se espera utilizar para dibujos 2D como circulos, rectangulos, elipses y otras figuras de geometría simple, en principio. El PasswordField es similar a una entrada de texto editable, con la diferencia que permite "esconder" los caracteres que en el se introducen, es decir, un campo de contraseñas, que se ha extendido del componente JPasswordField de Java. El Spinner de manera similar se ha extendido del componente JSpinner de Java. Y el AboutDialog es un cuadro de diálogo que contiene información acerca de la GUI, la idea y notación se ha tomado del componente del mismo nombre de la librería wxPython. Es muy probable que se añadan otros controles que puedan resultar útiles, desde luego "tomándolos prestados" de Java.

Otra parte interesante de GUIOOD Toolbox es que dispone de manejadores de posiciones o de distribución de componentes (layouts), los cuales ahorran tiempo significativo, dado que no hay necesidad de indicar las posiciones de los objetos gráficos de forma explícita. Los algoritmos de posicionamiento están en fase de desarrollo, siendo funcionales, pero con algunos detalles en cuanto al orden en que habrán de agregarse los componentes. Se dispone de 3 layouts: grid, vertical y horizontal. El primero distribuye los objetos utilizando filas y columnas como referencia, y el vertical y horizontal los distribuyen como se esperaría, dado el nombre.

Utilidades añadidas

GUIOOD permite exportar el contenido de una Table MATLAB a una tabla en HTML, y también a una hoja de cálculo Microsoft Excel.

El contenido de un Axes puede exportarse como imagen PNG, como un PDF, o incrustarla en un archivo HTML.

Estado del proyecto

El proyecto GUIOOD Toolbox comenzó a desarrollarse a principios de Noviembre de 2014, encontrándose ahora en una etapa muy temprana. Existen muchos detalles por agregar, como dar un mayor soporte al manejo de los eventos, un manejo de errores/excepciones un poco más personalizado, refinar los algoritmos de posicionamiento, escribir la documentación, y sobre todo mucho "testeo" del código. 

El plan inicial contempla un desarrollo durante seis meses. Por lo cual, se esperaría que para Mayo de 2015 pueda estar disponible una versión preliminar. ¿Por qué seis meses?, bueno, el calendario incluye muchos días festivos en este lapso.

Un ejemplo preeliminar (funcional)

A continuación se expone un fragmento de código totalmente funcional, y que deja ver más o menos la idea que se sigue y lo que se espera obtener:

function MiniCalc

% MiniCalc / Demo for GUIOOD Toolbox

%

% Author: Jorge De Los Santos

% Version: 0.1.0

% E-mail: delossantosmfq@gmail.com

% License: MIT License

app = Frame('Mini Calculadora',[220 100]);

app.SetLayout('grid',5,3,1); % Set main layout: grid. 5 rows and 3 columns

p1 = Panel();

p2 = Panel();

p3 = Panel();

app.AddMany(p1,p2,p3); % Add many panels to Frame (main app)

% Labels and TextFields

lb1 = Label('# 1');

lb2 = Label('# 2');

num1 = TextField();

num2 = TextField();

p1.AddMany(num1,lb1); % Add controls to Panel p1

p2.AddMany(num2,lb2); % Add controls to Panel p2

% Buttons

bt1 = Button('+');

bt2 = Button('-');

bt3 = Button('*');

bt4 = Button('/');

p3.AddMany(bt1,bt2,bt3,bt4); % Add buttons to panel p3

p3.SetLayout('horizontal',2); % Set layout for p3, horizontal and two controls

bt1.SetCallback(@calcular_fcn); % Set callback for buttons

bt2.SetCallback(@calcular_fcn);

bt3.SetCallback(@calcular_fcn);

bt4.SetCallback(@calcular_fcn);

    function calcular_fcn(~,~,obj)

        a = num1.GetText(); % Get value of "num1" Label

        b = num2.GetText(); % Get value of "num2" Label

        oper = obj.GetText(); % Get the operator of current Button clicked

        MessageBox(['Resultado = ',num2str(eval([a,oper,b]))],'GUIOOD');

    end

end

Si la GUI le parece "rara", no os preocupéis, cuestiones de temas del SO en que se ejecutó esta prueba.

Cualquier comentario o sugerencia  es siempre bienvenida. Y si desea colaborar con el proyecto no dude en contactar a los correos del blog (matlabtyp@gmail.com).

Ejecutar comandos del sistema operativo en MATLAB

Esta entrada tiene como objetivo mostrar la utilización de comandos nativos del sistema operativo desde el entorno de MATLAB. Pero ¿para qué utilizar comandos del SO?, para muchas cosas desde luego, podría necesitarse para ejecutar un script escrito en otro lenguaje de programación (Perl, Python,…), configurar variables del sistema, compilar y/o ejecutar un código fuente, entre otras muchas tareas.

MATLAB proporciona la función system que permite ejecutar cualquier instrucción soportada por el SO, la cual debe pasarse como un string, por ejemplo:

>> system('cd')

C:\Users\User\Documents\MATLAB\MATLAB TYP

ans =

     0

En lo anterior cd es un comando del sistema operativo que devuelve el directorio actual (tal como lo hace la función cd de MATLAB). Note que además de la cadena esperada se devuelve un valor cero guardado en la variable ans, esto sirve como identificador de status, indicando, en este caso, que el  comando ha sido ejecutado de forma satisfactoria.

Existe la alternativa de colocar un ampersand (&) al final de la instrucción para indicar que la respuesta del sistema se mostrará en una consola o terminal nativa, para el caso anterior sería:

>> system('cd&')

ans =

     0

Como se observa, simplemente se devuelve el status en el Command Window e inmediatamente se abre una consola mostrando el resultado de evaluar el comando del SO.

Para Microsoft Windows o sistemas basados en DOS existe la alternativa de usar el símbolo de exclamación de apertura (!) antecediendo a un comando, siguiendo con el mismo ejemplo:

>> !cd   

C:\Users\User\Documents\MATLAB\MATLAB TYP 

En este caso no se devuelve un status, lo cual nos llevaría a sugerir que si se requiere mayor robustez de código entonces habría que optar por el uso de la función system.

Abriendo programas de Microsoft Windows…

Utilizando system podemos acceder a programas nativos de Windows (Paint, Bloc de Notas, Recorte de pantalla, …). Para ello basta con pasar como argumento el nombre del programa, por ejemplo para abrir el Bloc de Notas:

>> system('notepad&');

O para la herramienta Recortes (Windows 7):

>> system('SnippingTool&');

Ejecutando un script Python…

Normalmente para ejecutar un script desarrollado en Python debería teclearse en una consola (o terminal) algo similar a esto:

> python nombre_script.py

Obviando el hecho de que estamos situados en la carpeta correspondiente para nuestro script python.

Usando la función system esto debería funcionar de la misma manera que se explicó anteriormente, así pues en MATLAB habría de introducirse lo siguiente:

>> system('python ejemplo.py&')

Donde ejemplo.py es el nombre del script. En este caso sí que es muy necesario adicionar el ampersand al final de la instrucción, para evitar cualquier tipo de incompatibilidad entre las salidas y entradas estándar de MATLAB y Python.

Modificando el color de línea de una gráfica generada con ezplot

La función ezplot es útil para trazar gráficas mediante una expresión definida simbólicamente o mediante una cadena de caracteres, lo cual, generalmente, facilita el trazo de las gráficas. Aunque lo más común es que un usuario de MATLAB comience utilizando la función plot para esta tarea, y con ello estará 'acostumbrado' a la posibilidad de incluir especificaciones de estilo, color y grosor de linea. Por ejemplo la siguiente instrucción trazará una gráfica de los vectores x e y utilizando una línea roja punteada:

plot(x,y,'r--');

No obstante, si se intenta hacer lo mismo con ezplot, MATLAB devolverá un error. La sintaxis más usual de ezplot es:

ezplot('f(x)', [a,b]);

Siendo a y b los extremos del intervalo a graficar. Ahora, se queremos personalizar la gráfica tendremos que hacer uso de la referencia (handle) a la linea graficada, para ello basta con asignar a una variable la instrucción de graficado, por ejemplo:

hL = ezplot('f(x)', [a,b]);

Con esta referencia guardada en la variable hL es posible utilizar la función set para modificar las propiedades de la linea. Véase el ejemplo siguiente:

hL = ezplot('sin(x)',[0 10]);

set(hL,'Color','r','LineStyle','--');

Calculo de un determinante mediante recursividad en MATLAB

El calculo de un determinante mediante recursividad o formalmente conocido como Teorema o Desarrollo de Laplace, consiste en calcular el determinante de una matriz cuadrada de $nxn$ mediante una descomposición en suma de determinantes menores, es decir, ir reduciendo en $n-1$ dimensiones. El desarrollo se puede hacer por filas o columnas.

La función recursiva para calcular el determinante utilizando el desarrollo en la primera fila puede expresarse como sigue:

Fuente: Wikipedia

Donde $a_{1,k}$ hace referencia al elemento ubicado en la primera fila y k-ésima columna, y $\alpha_{1,k}$ es el adjunto del elemento mencionado anteriormente.

Basado en la referencia anterior se implementó la siguiente función en MATLAB:

Ahora veamos un poco más detallado lo que implica cada línea de la función anterior: en la línea 2 se crea una vector idx cuyos valores son los números en el intervalo [1  n]  y que servirá para obtener, mediante un masking, los indices en fila y columna pertenecientes al adjunto correspondiente (véase linea 7 y 8). El ciclo for se implementa desde un valor unitario hasta el número de filas/columnas de la matriz de entrada X, y enseguida con la sentencia if  se comprueba si la matriz de entrada es de dimensiones unitarias (con lo cual se retorna la entrada misma) o bien si es de dimensiones mayores, con lo cual se implementa el algoritmo recursivo. Finalmente, habrán de sumarse todos los valores obtenidos en cada iteración del ciclo for, para ello se utiliza la función sum.

El costo de la recursividad

Por regla general, un algoritmo recursivo suele ser lento en ejecución. Por lo cual siempre es recomendable buscar o implementar otras técnicas de programación. En este caso, el ejemplo que hemos dado es puramente con fines didácticos, pero para mostrar un "poco" de lo ya dicho he decido "contar" el número de "llamadas" que se hacen a la función durante la ejecución para matrices de diversos tamaños. En la siguiente tabla se muestran las "llamadas" correspondientes para una matriz de $nxn$:

Dimensión de la matriz	Número de llamadas
1	1
2	3
3	10
4	41
5	206
6	1237
7	8660
8	69281

Como se observa el número de "llamadas" a la función crece de forma exponencial, lo cual se traduce en un gasto computacional considerable cuando las dimensiones de la matriz son mayores a un par de decenas e incluso menos. Se adjunta una gráfica correspondiente a la tabla anterior.

Sentencia continue en MATLAB

La sentencia continue es útil para controlar las ejecuciones dentro de un bucle, permite ignorar cualquier instrucción posterior al llamado de esta y continuar con el siguiente ciclo. Por ejemplo, véase el siguiente código:

for i=1:5

    disp(i);

    continue;

    disp(i^2);

end

Si ejecutamos lo anterior MATLAB imprimirá en pantalla los valores del 1 al 5, pero no llegará a "imprimir" los valores resultantes de elevarlos al cuadrado. Se preguntará el lector, esto para qué me sirve si pude no escribir las instrucciones posteriores o bien comentarlas para evitar su ejecución, y toda la razón tendrá, pero, ahora veamos un ejemplo más significativo y en el cual puede resultar más interesante la utilidad de continue:

for i=1:5

    ifrem(i,2)==0

        continue;

    end

    disp(i);

end

Revisemos lo anterior: al "correr" el script MATLAB nos devolverá en pantalla todos los números impares en el intervalo de ejecución, dado que si se cumple la condición de que el residuo de la división entera $i/2$ es nulo entonces ignorará la instrucción disp que se encuentra enseguida y pasará a ejecutarse la siguiente iteración.

La referencia "online" que proporciona MathWorks muestra un ejemplo del conteo de líneas de un archivo de texto, en el cual la sentencia continue se utiliza para evitar adicionar aquellas líneas en blanco. Puede ver el ejemplo en el siguiente link:

Sentencia continue

Leer y mostrar imágenes con MATLAB

De forma habitual, se utilizan las funciones del Image Processing Toolbox de MATLAB para importar, procesar y visualizar imágenes, más concretamente las funciones imread e imshow para leer y mostrar imágenes respectivamente. Pero además de las anteriores, puede utilizarse algunas funciones que forman parte del núcleo de MATLAB para dichas tareas, tales como importdata e image / imagesc, evidentemente pueden presentar ciertos inconvenientes, pero representan una alternativa en el caso de no contar con el toolbox requerido.

Leer una imagen con imread

La sintaxis de la función imread es muy sencilla, a saber:

>> imread('nombre_img','formato');

Donde nombre_img es el nombre de la imagen o bien la ruta completa de la imagen en el caso que no se encuentre en el Current Folder, formato es justamente eso: el tipo de imagen que vamos a leer (PNG, JPG, GIF, TIFF, etc...), es común omitir el segundo argumento e incluir, claro, la extensión del archivo en el nombre del mismo. Para ejemplificar utilizaré una imagen cuyo nombre es "img", en formato jpg y que se encuentra almacenada en el directorio actual de trabajo, luego para leer la imagen se tendría que hacer lo que a continuación se muestra:

>> X=imread('img.jpg');

Al teclear la instrucción anterior MATLAB crea una matriz X en la cual se guarda  la información de cada uno de los píxeles que componen la imagen. Podemos verificarlo utilizando el comando whos como sigue:

>> whos X

  Name        Size                Bytes  Class    Attributes

  X         300x400x3            360000  uint8       

Revisando lo que MATLAB nos devuelve podemos identificar que la matriz creada está compuesta de 300 filas, 400 columnas y tres capas o planos correspondientes al modelo de color RGB (Red, Green, Blue), es decir, cada capa corresponde a la intensidad de cada uno de los colores. Además, la clase de datos utilizados son uint8 (entero sin signo de 8 bits) cuyo rango es de 0 a 255.


Mostrar una imagen con imshow

Una vez se ha leído y almacenado la imagen podemos utilizar la función imshow para visualizarla, la sintaxis de esta función es:

>> imshow(IMG);

Donde IMG es la matriz en la cual se ha guardado la información referente a la imagen. Para nuestro caso:

>> imshow(X);

Utilizando importdata e imagesc

Además de imread, es posible leer una imagen utilizando la función importdata, la sintaxis es:

>> X=importdata('nombre_img');

Para el ejemplo que hemos utilizado:

>> X=importdata('img.jpg');

Una vez almacenada la imagen podemos utilizar la función imagesc para mostrar la imagen:

>> imagesc(X);

Y como tal, el objetivo de esta entrada era simplemente adquirir y visualizar las imágenes. En posteriores entradas se hará referencia a algunas operaciones básicas que pueden aplicarse a una imagen, o mejor dicho, a la matriz que guarda la información de la misma.

Graficar inecuaciones / desigualdades en MATLAB

Una inecuación es una desigualdad algebraica que contiene una o más incógnitas, ejemplos de estas son las siguientes:

$$x^2+y^2>2$$
$$x+3>y$$
$$x^3+7<1$$

MATLAB no tiene soporte nativo para graficar desigualdades, pero evidentemente pueden implementarse soluciones mediante comparadores que evalúen los valores tomados por una cierta expresión en una región especificada. La siguiente función llamada inecgraf permite llevar a cabo dicha tarea:

function varargout = inecgraf(I,R)

% Grafica una desigualdad (inecuación) en un rango

% especificado.

%

% Argumentos de entrada:

%            I    -   Inecuación

%            R    -   Rango en el cual se trazará la

%                     gráfica.

%

% Argumentos de salida:

%            h    -   Si se especifica un argumento

%                     salida, la función devuelve un

%                     array de handles que le permite

%                     modificar las propiedades de la

%                     gráfica de salida. (Véase ejemplos).

%

% Ejemplos: 

%           >> inecgraf('x.^2+y.^2<10',[-5 5]);

%           >> h = inecgraf('y<x+3',[0 10]);

%           >> set(h,'color','r','MarkerSize',5);

%

% || Por: Jorge De Los Santos ||

% || Rev. 1.0  ||  Fecha: 06/05/14 ||

set(gca,'NextPlot','add');

axis([R(1) R(2) R(1) R(2)]);

dd=(R(2)-R(1))/50;

[x,y]=meshgrid(R(1):dd:R(2));

[f,c]=find(eval(I));

h=zeros(1,length(f));

for i=1:length(f)

    h(i)=plot(x(f(i),c(i)),y(f(i),c(i)),'b*','MarkerSize',2);

end

if nargout==1

    varargout{1}=h;

end

end

Las instrucciones de uso se muestran en la descripción de la función, enseguida se muestran los ejemplos obtenidos para las inecuaciones que se indican:

>> inecgraf('y>x.^2-2',[-5 5]);

>> inecgraf('x.^2+y.^2>5',[-5 5]);

¿ MATLAB o Maple ?

¿Por qué MATLAB?, ¿Por qué Maple? o ¿Cuando utilizar MATLAB, o Maple?, son quizá algunas de las interrogantes respecto a este "dilema" que a más de uno le han surgido. 

Para comenzar, ambos programas fueron desarrollados allá por la década de los 80's: Maple en 1981 en Canadá y MATLAB en 1984 en EEUU. Orientados ambos a resolver problemas de matemáticas e ingeniería, no obstante, existen diferencias muy notorias: Maple está más especializado en el área del cálculo simbólico y el álgebra computacional, y MATLAB en la computación numérica y el desarrollo de modelos y simulaciones para ingeniería.

A experiencia propia, cuando ingresé al nivel universitario hace unos años, me vi pronto en la necesidad (como casi todos, imagino) de buscar un software que me permitiera hacer más llevaderos mis cursos de matemáticas, siendo las primeras tareas el trazar gráficas, resolver sistemas de ecuaciones y/o derivadas e integrales, cosas de esas. Comencé en un primer intento utilizando Geogebra, un programa muy ligero, fácil de utilizar y sobre todo gratis, pero pronto dejo de ser útil para mis propósitos (en ese entonces Geogebra no tenía herramientas de CAS). En esa búsqueda me cruce con Matemáticas de Microsoft (Versión 2009), pero de la misma forma pronto dejo de ser lo suficientemente útil. Para ese entonces tenía en mi lista de seguimiento algunos de los programas más comunes: Derive, Mathematica, MATLAB, Maple e incluso Octave. Después de escuchar sugerencias e 'investigar' un poco acerca de los mismos, me decidí por comenzar a utilizar Maple, y bueno, a decir verdad quedé maravillado, todo era más simple con Maple y además ¿qué no podía resolver Maple?, lo hacía todo.

Poco después, y por obligación, llego MATLAB, era el lenguaje de programación que utilizaría en mi curso de Métodos Numéricos. Al principio me pareció  poco "amigable" y más aun porque la versión que utilizaba (R2008a) no disponía de un toolbox de Matemáticas Simbólicas, así que no podía realizar operación algebraica de ningún tipo, lo cual no representaba limitación alguna para cubrir el curso que estaba llevando.

Pero bueno, en ese entonces estaba muy "verde" como para comprender la utilidad real de un programa tan potente como MATLAB. Le abandoné unos meses, hasta que por necesidad tuve que recurrir a este nuevamente para implementar algoritmos de simulaciones numéricas en un curso de Resistencia de Materiales. 

DE LA PROGRAMACIÓN...

Como mencioné anteriormente, tuve que recurrir a MATLAB para desarrollar algoritmos, y me pareció realmente sencillo de utilizar. Llevar un pseudocódigo a MATLAB resulta muy eficaz en cuestión de tiempo de implementación, además de que la curva de aprendizaje del lenguaje es muy rápida. En cambio, utilizar Maple para implementar un algoritmo es una tarea un poco desalentadora en principio, cuesta un poco más comprender la sintaxis del lenguaje. Probablemente lo anterior se deba a que MATLAB tiene muchas similitudes con un lenguaje de programación tan popular como C, en cambio Maple tiene una sintaxis muy distinta a C y más afín a lenguajes como Modula.

DE LAS INTERFACES GRÁFICAS...

En MATLAB se pueden desarrollar interfaces gráficas de una calidad aceptable y con una facilidad "tremenda", incluso con el entorno de desarrollo (GUIDE) la tarea se vuelve mucho más sencilla. Maple, también proporciona un entorno de desarrollo para Maplets (interfaces gráficas creadas en Maple), pero la documentación disponible es muy limitada, lo cual hace aún más complicado el desarrollo de las mismas.

DE LA DOCUMENTACIÓN...

Tanto MATLAB como Maple proporcionan una documentación muy extensa, con ejemplos para cada una de sus funciones, demos e incluso vídeo tutoriales en el sitio web oficial de cada uno. No obstante, en cuanto a información existente escrita por terceros, es innegable que MATLAB dispone de mucha más información, consecuencia directa del número de usuarios de cada uno de los programas.

EN RESUMEN...

Puede sonar demasiado obvio, pero lo cierto es que la elección dependerá del uso que se le dará al programa. Maple puede resultar muy útil para resolver todo tipo de problemas que involucren cálculo simbólico, en eso no hay discusión, además como herramienta didáctica en problemas de matemáticas resulta totalmente adecuado, debido a su fácil manejo y a la forma en que presenta sus resultados. MATLAB, por el contrario, resultará más útil para aplicaciones que requieran el manejo de técnicas numéricas, para desarrollar algoritmos y/o simulaciones e incluso para procesar datos que provienen de una aplicación externa.