Leer y mostrar imágenes con MATLAB

De forma habitual, se utilizan las funciones del Image Processing Toolbox de MATLAB para importar, procesar y visualizar imágenes, más concretamente las funciones imread e imshow para leer y mostrar imágenes respectivamente. Pero además de las anteriores, puede utilizarse algunas funciones que forman parte del núcleo de MATLAB para dichas tareas, tales como importdata e image / imagesc, evidentemente pueden presentar ciertos inconvenientes, pero representan una alternativa en el caso de no contar con el toolbox requerido.

Leer una imagen con imread

La sintaxis de la función imread es muy sencilla, a saber:

>> imread('nombre_img','formato');

Donde nombre_img es el nombre de la imagen o bien la ruta completa de la imagen en el caso que no se encuentre en el Current Folder, formato es justamente eso: el tipo de imagen que vamos a leer (PNG, JPG, GIF, TIFF, etc...), es común omitir el segundo argumento e incluir, claro, la extensión del archivo en el nombre del mismo. Para ejemplificar utilizaré una imagen cuyo nombre es "img", en formato jpg y que se encuentra almacenada en el directorio actual de trabajo, luego para leer la imagen se tendría que hacer lo que a continuación se muestra:

>> X=imread('img.jpg');

Al teclear la instrucción anterior MATLAB crea una matriz X en la cual se guarda  la información de cada uno de los píxeles que componen la imagen. Podemos verificarlo utilizando el comando whos como sigue:

>> whos X

  Name        Size                Bytes  Class    Attributes

  X         300x400x3            360000  uint8       

Revisando lo que MATLAB nos devuelve podemos identificar que la matriz creada está compuesta de 300 filas, 400 columnas y tres capas o planos correspondientes al modelo de color RGB (Red, Green, Blue), es decir, cada capa corresponde a la intensidad de cada uno de los colores. Además, la clase de datos utilizados son uint8 (entero sin signo de 8 bits) cuyo rango es de 0 a 255.


Mostrar una imagen con imshow

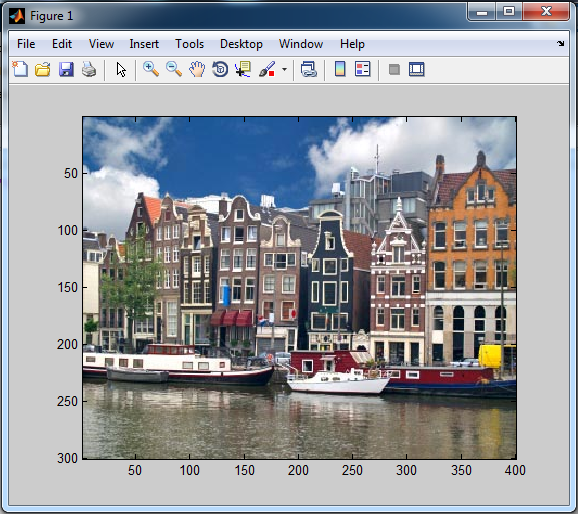
Una vez se ha leído y almacenado la imagen podemos utilizar la función imshow para visualizarla, la sintaxis de esta función es:

>> imshow(IMG);

Donde IMG es la matriz en la cual se ha guardado la información referente a la imagen. Para nuestro caso:

>> imshow(X);

Utilizando importdata e imagesc

Además de imread, es posible leer una imagen utilizando la función importdata, la sintaxis es:

>> X=importdata('nombre_img');

Para el ejemplo que hemos utilizado:

>> X=importdata('img.jpg');

Una vez almacenada la imagen podemos utilizar la función imagesc para mostrar la imagen:

>> imagesc(X);

Y como tal, el objetivo de esta entrada era simplemente adquirir y visualizar las imágenes. En posteriores entradas se hará referencia a algunas operaciones básicas que pueden aplicarse a una imagen, o mejor dicho, a la matriz que guarda la información de la misma.

Graficar inecuaciones / desigualdades en MATLAB

Una inecuación es una desigualdad algebraica que contiene una o más incógnitas, ejemplos de estas son las siguientes:

$$x^2+y^2>2$$
$$x+3>y$$
$$x^3+7<1$$

MATLAB no tiene soporte nativo para graficar desigualdades, pero evidentemente pueden implementarse soluciones mediante comparadores que evalúen los valores tomados por una cierta expresión en una región especificada. La siguiente función llamada inecgraf permite llevar a cabo dicha tarea:

function varargout = inecgraf(I,R)

% Grafica una desigualdad (inecuación) en un rango

% especificado.

%

% Argumentos de entrada:

%            I    -   Inecuación

%            R    -   Rango en el cual se trazará la

%                     gráfica.

%

% Argumentos de salida:

%            h    -   Si se especifica un argumento

%                     salida, la función devuelve un

%                     array de handles que le permite

%                     modificar las propiedades de la

%                     gráfica de salida. (Véase ejemplos).

%

% Ejemplos: 

%           >> inecgraf('x.^2+y.^2<10',[-5 5]);

%           >> h = inecgraf('y<x+3',[0 10]);

%           >> set(h,'color','r','MarkerSize',5);

%

% || Por: Jorge De Los Santos ||

% || Rev. 1.0  ||  Fecha: 06/05/14 ||

set(gca,'NextPlot','add');

axis([R(1) R(2) R(1) R(2)]);

dd=(R(2)-R(1))/50;

[x,y]=meshgrid(R(1):dd:R(2));

[f,c]=find(eval(I));

h=zeros(1,length(f));

for i=1:length(f)

    h(i)=plot(x(f(i),c(i)),y(f(i),c(i)),'b*','MarkerSize',2);

end

if nargout==1

    varargout{1}=h;

end

end

Las instrucciones de uso se muestran en la descripción de la función, enseguida se muestran los ejemplos obtenidos para las inecuaciones que se indican:

>> inecgraf('y>x.^2-2',[-5 5]);

>> inecgraf('x.^2+y.^2>5',[-5 5]);

¿ MATLAB o Maple ?

¿Por qué MATLAB?, ¿Por qué Maple? o ¿Cuando utilizar MATLAB, o Maple?, son quizá algunas de las interrogantes respecto a este "dilema" que a más de uno le han surgido. 

Para comenzar, ambos programas fueron desarrollados allá por la década de los 80's: Maple en 1981 en Canadá y MATLAB en 1984 en EEUU. Orientados ambos a resolver problemas de matemáticas e ingeniería, no obstante, existen diferencias muy notorias: Maple está más especializado en el área del cálculo simbólico y el álgebra computacional, y MATLAB en la computación numérica y el desarrollo de modelos y simulaciones para ingeniería.

A experiencia propia, cuando ingresé al nivel universitario hace unos años, me vi pronto en la necesidad (como casi todos, imagino) de buscar un software que me permitiera hacer más llevaderos mis cursos de matemáticas, siendo las primeras tareas el trazar gráficas, resolver sistemas de ecuaciones y/o derivadas e integrales, cosas de esas. Comencé en un primer intento utilizando Geogebra, un programa muy ligero, fácil de utilizar y sobre todo gratis, pero pronto dejo de ser útil para mis propósitos (en ese entonces Geogebra no tenía herramientas de CAS). En esa búsqueda me cruce con Matemáticas de Microsoft (Versión 2009), pero de la misma forma pronto dejo de ser lo suficientemente útil. Para ese entonces tenía en mi lista de seguimiento algunos de los programas más comunes: Derive, Mathematica, MATLAB, Maple e incluso Octave. Después de escuchar sugerencias e 'investigar' un poco acerca de los mismos, me decidí por comenzar a utilizar Maple, y bueno, a decir verdad quedé maravillado, todo era más simple con Maple y además ¿qué no podía resolver Maple?, lo hacía todo.

Poco después, y por obligación, llego MATLAB, era el lenguaje de programación que utilizaría en mi curso de Métodos Numéricos. Al principio me pareció  poco "amigable" y más aun porque la versión que utilizaba (R2008a) no disponía de un toolbox de Matemáticas Simbólicas, así que no podía realizar operación algebraica de ningún tipo, lo cual no representaba limitación alguna para cubrir el curso que estaba llevando.

Pero bueno, en ese entonces estaba muy "verde" como para comprender la utilidad real de un programa tan potente como MATLAB. Le abandoné unos meses, hasta que por necesidad tuve que recurrir a este nuevamente para implementar algoritmos de simulaciones numéricas en un curso de Resistencia de Materiales. 

DE LA PROGRAMACIÓN...

Como mencioné anteriormente, tuve que recurrir a MATLAB para desarrollar algoritmos, y me pareció realmente sencillo de utilizar. Llevar un pseudocódigo a MATLAB resulta muy eficaz en cuestión de tiempo de implementación, además de que la curva de aprendizaje del lenguaje es muy rápida. En cambio, utilizar Maple para implementar un algoritmo es una tarea un poco desalentadora en principio, cuesta un poco más comprender la sintaxis del lenguaje. Probablemente lo anterior se deba a que MATLAB tiene muchas similitudes con un lenguaje de programación tan popular como C, en cambio Maple tiene una sintaxis muy distinta a C y más afín a lenguajes como Modula.

DE LAS INTERFACES GRÁFICAS...

En MATLAB se pueden desarrollar interfaces gráficas de una calidad aceptable y con una facilidad "tremenda", incluso con el entorno de desarrollo (GUIDE) la tarea se vuelve mucho más sencilla. Maple, también proporciona un entorno de desarrollo para Maplets (interfaces gráficas creadas en Maple), pero la documentación disponible es muy limitada, lo cual hace aún más complicado el desarrollo de las mismas.

DE LA DOCUMENTACIÓN...

Tanto MATLAB como Maple proporcionan una documentación muy extensa, con ejemplos para cada una de sus funciones, demos e incluso vídeo tutoriales en el sitio web oficial de cada uno. No obstante, en cuanto a información existente escrita por terceros, es innegable que MATLAB dispone de mucha más información, consecuencia directa del número de usuarios de cada uno de los programas.

EN RESUMEN...

Puede sonar demasiado obvio, pero lo cierto es que la elección dependerá del uso que se le dará al programa. Maple puede resultar muy útil para resolver todo tipo de problemas que involucren cálculo simbólico, en eso no hay discusión, además como herramienta didáctica en problemas de matemáticas resulta totalmente adecuado, debido a su fácil manejo y a la forma en que presenta sus resultados. MATLAB, por el contrario, resultará más útil para aplicaciones que requieran el manejo de técnicas numéricas, para desarrollar algoritmos y/o simulaciones e incluso para procesar datos que provienen de una aplicación externa. 

Graficando un "toro" en MATLAB

Un toro es una superficie o sólido de revolución generado por la rotación de una circunferencia alrededor de un eje determinado.

Para nuestro caso utilizaremos la circunferencia de radio 1 y coordenadas de centro (1,2), cuya ecuación en coordenadas cartesianas sería:

$$(x-1)^2+(y-2)^2=1$$

La ecuación anterior está dada de forma implícita, pero para nuestros fines necesitamos la función de la circunferencia de forma explícita, lo cual nos conduce a despejar la variable dependiente "y" y expresar la circunferencia mediante las dos funciones que se muestran enseguida:

$$ \left\{ \begin{array}{cc} y_1=\sqrt{1-(x-1)^2}+2 \\ y_2=-\sqrt{1-(x-1)^2}+2 \end{array} \right. $$

Una vez comprendido lo anterior, podemos centrarnos en la función cylinder nativa de MATLAB que nos permite generar un sólido de revolución mediante la sintaxis:

>> cylinder(fun);

Donde "fun" es una función $f(x)$ y que sirve para establecer el perfil del sólido de revolución. Regresando a nuestro objetivo principal, enseguida se muestra el código necesario para generar la gráfica de un toro, utilizando las dos funciones mencionadas con anterioridad:

x=0:0.1:2;

f1=sqrt(1-(x-1).^2)+2;

f2=-sqrt(1-(x-1).^2)+2;

hold on

cylinder(f1);

cylinder(f2);

daspect([1 1 1]);

view(3);